Formelsammlung: Unterschied zwischen den Versionen
Ralph (Diskussion | Beiträge) |
Ralph (Diskussion | Beiträge) (→Fläche) |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 72: | Zeile 72: | ||
== Zwölfeck == | == Zwölfeck == | ||
Die Grundfläche der Jurte entspricht einem regelmässigen [[Zwölfeck]] | Die Grundfläche der Jurte entspricht einem regelmässigen [[Zwölfeck]]. Eine zwölfeckige Jurte mit einem Durchmesser von 6 m hat eine Grundfläche von 27 m² | ||
==== Zentriwinkel ==== | ==== Zentriwinkel ==== | ||
| Zeile 114: | Zeile 114: | ||
<math>A=r^2\cdot\frac{2}{1}\cdot\frac{2}{\sqrt{2}}\cdot\frac{2}{\sqrt{2+\sqrt{2}}}=4r^2\sqrt{2-\sqrt{2}}.</math> | <math>A=r^2\cdot\frac{2}{1}\cdot\frac{2}{\sqrt{2}}\cdot\frac{2}{\sqrt{2+\sqrt{2}}}=4r^2\sqrt{2-\sqrt{2}}.</math> | ||
[ | |||
== Achtzehneck == | |||
Die Grundfläche der [[Giga-Großjurte]] entspricht einem [[Achtzehneck]] | |||
==== Zentriwinkel ==== | |||
<math> \alpha = \frac{360^\circ}{18} = 20^\circ </math> | |||
==== Innenwinkel ==== | |||
Der Innenwinkel eines regelmäßigen Sechzehneck hat 160°, und die Summe der Innenwinkel beträgt 2880°. | |||
<math> \delta = 180^\circ - \alpha = 160^\circ </math> | |||
==== Fläche ==== | |||
<math> A = \frac{18}{4} \cdot a^2 \cdot \frac{\cos 10^\circ}{\sin 10^\circ}</math> | |||
<math> A = \frac{18}{2} \cdot r_u^2 \cdot \sin 20^\circ </math> | |||
== Dreieck == | == Dreieck == | ||
| Zeile 197: | Zeile 212: | ||
<math>s = \sqrt{h^{2}+r^{2}}</math> | <math>s = \sqrt{h^{2}+r^{2}}</math> | ||
==== Winkel | ==== Winkel ==== | ||
eines geraden Kreiskegels ist der halbe Öffnungswinkel, auch ''halber Kegelwinkel'' genannt | eines geraden Kreiskegels ist der halbe Öffnungswinkel, auch ''halber Kegelwinkel'' genannt | ||
Aktuelle Version vom 27. November 2018, 09:31 Uhr
Wer gerne mit Kohte und Jurte konstruiert und sich dazu gerne Pläne macht, der kommt um ein gewisses Maß an Mathematik nicht herum. Idealisiert sind Kohte und Jurte regelmäßige Vielecke. Das modulare System lässt zu, unterschiedliche Planen fast beliebig zu kombinieren. Daraus ergeben sich vielfältige geometrische Formen. Zu deren Berechnung folgt unten die nötige Formelsammlung. Für die Bedeutung der Abkürzungen und Werte siehe: Wichtige Maße.
entspricht der Länge einer Viereckzeltbahn und somit der Seitenlänge von Achteck (Kohte), Zwölfeck (Jurte), Sechzehneck (Großjurte), usw.
Den theoretischen Wert von nehmen wir wie folgt an:
- Tortuga / Stromeyer
- Schlaufenjurte
- Rainbow
Sechseck
Die Grundfläche der Rainbow-Kohte entspricht einem regelmässigen Sechseck
Umkreisradius
Inkreisradius
Flächeninhalt
Diagonale über 2 (bzw. 4) Seiten
Diagonale über 3 Seiten (Durchmesser)
Innenwinkel
Achteck
Die Grundfläche der Kohte entspricht einem gleichseitigem Achteck.
Inkreisradius
Umkreisradius
Große Diagonale (Durchmesser)
Mittlere Diagonale
Kleine Diagonale
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle d_3 = a \ \sqrt{2 + \sqrt{2}} \ = \ R \, \sqrt{2} }
Zentriwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \frac{360^\circ}{8} = 45^\circ }
Innenwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \delta = 180^\circ - \alpha = 135^\circ }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \cos \delta = \frac{-1}{\sqrt{2}} }
Flächeninhalt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = a^2 \ (2+ 2 \sqrt{2})}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = r_u^2 \ 2 \sqrt{2}}
Zwölfeck
Die Grundfläche der Jurte entspricht einem regelmässigen Zwölfeck. Eine zwölfeckige Jurte mit einem Durchmesser von 6 m hat eine Grundfläche von 27 m²
Zentriwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \frac{360^\circ}{12} = 30^\circ }
Innenwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \delta = 180^\circ - \alpha = 150^\circ }
Flächeninhalt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} A & = 3 \cot\left(\frac{\pi}{12} \right) a^2 = 3 \left(2+\sqrt{3} \right) a^2 \\ & \approx 11{,}19615\,a^2. \end{align}}
Die Fläche kann auch mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} als dem Radius des Umkreises[1] berechnet werden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = 6 \sin\left(\frac{\pi}{6}\right) R^2 = 3 R^2.}
Mit r als Radius des Inkreises, ergibt sich der Flächeninhalt des regelmäßigen Zwölfecks zu
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \begin{align} A & = 12 \tan\left(\frac{\pi}{12}\right) r^2 = 12 \left(2-\sqrt{3} \right) r^2 \\ & \approx 3{,}21539\,r^2. \end{align}}
Sechzehneck
Die Grundfläche der Großjurte entspricht einem Sechzehneck
Zentriwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \frac{360^\circ}{16} = 22,5^\circ }
Innenwinkel
Der Innenwinkel eines regelmäßigen Sechzehneck hat 157,5°, und die Summe der Innenwinkel beträgt 2520°.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \delta = 180^\circ - \alpha = 157,5^\circ }
Flächeninhalt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = 4a^2 \cot \frac{\pi}{16} = 4a^2 (\sqrt{2}+1)\left(\sqrt{4-2\sqrt{2}}+1\right)}
Da die Anzahl der Seiten eines Sechzehnecks eine Zweierpotenz ist, kann die Fläche auch über den Umkreis mit dem Radius Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r} durch eine abgeleitete Formel aus Vietas Produktdarstellung der Kreiszahl Pi berechnet werden.[2]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A=r^2\cdot\frac{2}{1}\cdot\frac{2}{\sqrt{2}}\cdot\frac{2}{\sqrt{2+\sqrt{2}}}=4r^2\sqrt{2-\sqrt{2}}.}
Achtzehneck
Die Grundfläche der Giga-Großjurte entspricht einem Achtzehneck
Zentriwinkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \frac{360^\circ}{18} = 20^\circ }
Innenwinkel
Der Innenwinkel eines regelmäßigen Sechzehneck hat 160°, und die Summe der Innenwinkel beträgt 2880°.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \delta = 180^\circ - \alpha = 160^\circ }
Fläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = \frac{18}{4} \cdot a^2 \cdot \frac{\cos 10^\circ}{\sin 10^\circ}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A = \frac{18}{2} \cdot r_u^2 \cdot \sin 20^\circ }
Dreieck
Bei den Formeln für das Dreieck entspricht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} nicht der Kantenlänge eine Plane (außer es geht um die Dreieckzeltbahn)!
gleichschenkliges Dreieck
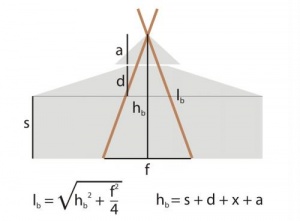
Mit diesen Formeln kann z.B. die Bundhöhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h_b } für die Mittelstangen einer Jurte bestimmt werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h_b = s+d+x+a } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s } = Seitenhöhe der Jurte, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle d } = Dacherhöhung, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x } = Abstand Dach zu Abdeckplane und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a } = Höhe Abdeckplane
Wenn wir jetzt noch einen Abstand der beiden Mittelstangen für die Feuerstelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f } festlegen, dann können wir mit der Formel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle l_b = \sqrt{h_b^2 + \frac{f^2}{4}} } die Länge der Mittelstangen, bzw. wo dort der Bund liegen soll, bestimmen.
Seitenlänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a = b }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle c^2 = 2a^2(1-\cos(\gamma)) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle c = 2a\cdot \sin\left(\frac{\gamma}{2}\right) }
Höhe
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h_c = \sqrt{a^2 - \frac{1}{4}c^2} }
Umfang
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle U \, = \, 2a + c }
Winkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \beta, \,\gamma = 180^\circ -2 \alpha }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \gamma = \arccos \left( 1- \frac{c^2}{2a^2}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \gamma = 2\arcsin\left(\frac{c}{2a}\right) }
Flächeninhalt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A \, = \, \frac{c}{2}\sqrt{a^2-\frac{c^2}{4}} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A \, = \, \frac{1}{2}\,c\cdot h_c}
gleichseitiges Dreieck
Seitenlänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a = b = c \,}
Winkel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \alpha = \beta = \gamma = 60^\circ }
Höhe
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h=\frac{\sqrt{3}}{2}a }
Flächeninhalt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A \, = \, \frac{a^2\sqrt{3}}{4} }
Umfang
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle u \, = \, 3 \cdot a }
Umkreisradius
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r_U \, = \, \frac{\sqrt{3}}{3}a }
Inkreisradius
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r_I \, = \, \frac{\sqrt{3}}{6}a = \frac 1 2 \cdot r_U }
Pyramide
regelmäßige Pyramide
- Kohte = regelmäßige achtseitige Pyramide
- Jurtendach = regelmäßige zwölfseitige Pyramide
regelmäßige dreiseitige Pyramide
Ein Anwendungsfall für eine regelmäßige dreiseitige Pyramide ist das Dreibein in oder außerhalb einer Jurte.
Formeln für einen Kegel
Ein Kegel beschreibt am besten die Hüllfläche eines Dreibein. Damit lassen sich z.B. die benötigten Stangenlängen und der Platzbedarf für ein Außendreibein berechnen.
gerader Kreiskegel
Radius
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r = \sqrt{s^{2}-h^{2}}}
Höhe
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h = \sqrt{s^{2}-r^{2}}}
Mantellinie
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s = \sqrt{h^{2}+r^{2}}}
Winkel
eines geraden Kreiskegels ist der halbe Öffnungswinkel, auch halber Kegelwinkel genannt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sin\varphi = \frac{\text{Gegenkathete von }\varphi}{\text{Hypotenuse}} = \frac{r}{s}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \tan\varphi = \frac{\text{Gegenkathete von }\varphi}{\text{Ankathete von }\varphi} = \frac{r}{h}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \varphi = \arcsin\frac{r}{s} = \arctan\frac{r}{h}}
Durchmesser der Grundfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle d = 2 \cdot r = 2 \cdot h \cdot \tan\varphi}
Grundfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_G = r^2\cdot \pi }
Flächeninhalt der Mantelfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_M = r\cdot s\cdot \pi}
Oberfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A_O = A_G + A_M = r\cdot\pi\cdot (r + s)}
Volumen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V = \frac{1}{3}\cdot \pi\cdot r^{2}\cdot h = \frac{1}{3}\cdot A_G \cdot h}
Kegelstumpf
Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r} werde der Radius der Deckfläche, mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} der Radius der Grundfläche bezeichnet. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \varphi} sei der Winkel zwischen einer Mantellinie und der Kegelachse.
Volumen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V = \frac{h \cdot \pi}{3} \cdot (R^2 + R \cdot r + r^2)}
Länge einer Mantellinie
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m = \sqrt{(R-r)^2 + h^2}}
Mantelfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle M = (R+r) \cdot \pi \cdot m}
Deckfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle D = \pi \cdot r^2}
Grundfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle G = \pi \cdot R^2}
Oberfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle O = \pi \cdot \left[ r^2 + R^2 + m \cdot (r + R) \right]}
Höhe des Kegelstumpfs
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h=\frac{R-r}{\tan\varphi}}
Anmerkungen
Innenwinkel
Der Innenwinkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \delta } entspricht zum Beispiel dem Maß der Winkel für das Jurtengerüst.
Fläche
Die Flächenberechnung ist z.B. dort hilfreich, wo Jurten kombiniert werden, aber dennoch die Grenze zu Fliegenden Bauten nicht überschritten werden soll.
Einzelnachweise
- ↑ Siehe József Kürscháks geometrischen Beweis the Wolfram Demonstration Project
- ↑ Vietas Produktdarstellung der Kreiszahl Pi