Außendreibein

Jurte mit Außendreibein

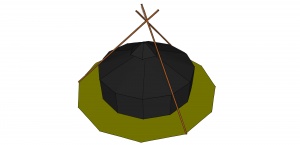
Um eine Jurte im Inneren völlig frei von Stangen zu halten, ist ein Außendreibein eine praktikable Lösung, sofern längeres Stangenholz zu Verfügung steht.

Welche Stangenlänge benötigt es hierfür?

Annahme: Aufstellwinkel der Stangen = 45°

In unserer Vorstellung zerlegen wir die benötigte Stangenlänge in einen Teil über der Traufkante einer Jurte und in den Teil unter der Traufkante der Jurte. so betrachten wir einmal einen gedachten Kegel und einmal einen Kegelstumpf.

In den Formeln heißen diese Strecken für die Stangenlängen Mantellinie.

$s_{o}$ entspricht der oberen Länge

$s_{u}$ entspricht der unteren Länge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} entspricht dem Durchmesser der Jurte

Für die Höhe des oberen Kegels lautet die Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h = \sqrt{s_o^{2}-R^{2}}}

Formeln für einen Kegel

gerader Kreiskegel

Radius

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle r = \sqrt{s^{2}-h^{2}}}

Höhe

$h={\sqrt {s^{2}-r^{2}}}$

Mantellinie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s = \sqrt{h^{2}+r^{2}}}

Winkel $\varphi$

eines geraden Kreiskegels ist der halbe Öffnungswinkel, auch halber Kegelwinkel genannt

Anwendung der trigonometrischen Funktionen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \sin\varphi = \frac{\text{Gegenkathete von }\varphi}{\text{Hypotenuse}} = \frac{r}{s}}

$\tan \varphi ={\frac {{\text{Gegenkathete von }}\varphi }{{\text{Ankathete von }}\varphi }}={\frac {r}{h}}$

$\varphi =\arcsin {\frac {r}{s}}=\arctan {\frac {r}{h}}$

Durchmesser der Grundfläche

$d=2\cdot r=2\cdot h\cdot \tan \varphi$

Grundfläche

$A_{G}=r^{2}\cdot \pi$

Flächeninhalt der Mantelfläche

$A_{M}=r\cdot s\cdot \pi$

Oberfläche

$A_{O}=A_{G}+A_{M}=r\cdot \pi \cdot (r+s)$

Volumen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle V = \frac{1}{3}\cdot \pi\cdot r^{2}\cdot h = \frac{1}{3}\cdot A_G \cdot h}

Kegelstumpf

Kegelstumpf,
Definition der Höhe

Mit $r$ werde der Radius der Deckfläche, mit $R$ der Radius der Grundfläche bezeichnet. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \varphi} sei der Winkel zwischen einer Mantellinie und der Kegelachse.

Volumen

$V={\frac {h\cdot \pi }{3}}\cdot (R^{2}+R\cdot r+r^{2})$

Länge einer Mantellinie

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m = \sqrt{(R-r)^2 + h^2}}

Mantelfläche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle M = (R+r) \cdot \pi \cdot m}

Deckfläche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle D = \pi \cdot r^2}

Grundfläche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle G = \pi \cdot R^2}

Oberfläche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle O = \pi \cdot \left[ r^2 + R^2 + m \cdot (r + R) \right]}

Höhe des Kegelstumpfs

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle h=\frac{R-r}{\tan\varphi}}