Außendreibein: Unterschied zwischen den Versionen

Aktuelle Version vom 5. Juni 2022, 19:54 Uhr

Jurte mit Außendreibein, Foto: Felix Be

Jurte mit Außendreibein, Foto: Ka Be

Jurte mit Außendreibein

Abbildung zur Formel

Um eine Jurte im Inneren völlig frei von Stangen zu halten, ist ein Außendreibein eine praktikable Lösung, sofern längeres Stangenholz zu Verfügung steht.

Welche Stangenlänge benötigt es hierfür?

Annahme: Aufstellwinkel der Stangen $\varphi =45^{\circ }$

In unserer Vorstellung zerlegen wir die benötigte Stangenlänge in einen Teil über der Traufkante einer Jurte und in den Teil unter der Traufkante der Jurte. So betrachten wir einmal einen gedachten Kegel und einmal einen Kegelstumpf.

In den Formeln für einen Kegel heißen diese Strecken für die Stangenlängen Mantellinie. Diese Formeln findest du in unserer Formelsammlung.

$s_{o}$ entspricht der oberen Länge

$s_{u}$ entspricht der unteren Länge

$R$ entspricht dem Durchmesser der Jurte

$h_{u}$ entspricht der Seitenhöhe der Jurte

Für die Höhe des oberen Kegels lautet die Formel $h_{o}={\sqrt {s_{o}^{2}-R^{2}}}$ . Stellen wir diese Formel um nach $s_{o}$ , so erhalten wir $s_{o}={\sqrt {h_{o}^{2}+R^{2}}}$ .

Nehmen wir nun einen optimalen Winkel mit $\varphi =45^{\circ }$ an, so ist $h_{o}=R$ . Aus unserer Formel wird $s_{o}={\sqrt {2}}\cdot R$

Nun brauchen wir noch den unteren Teil.

Für $s_{u}$ gilt $s_{u}={\sqrt {(R_{u}-R)^{2}+h_{u}^{2}}}$ . Weiter gilt die Annahme $\varphi =45^{\circ }$ . Daraus folgt: $R_{u}=R+h_{u}$ und $s_{u}={\sqrt {2}}\cdot h_{u}^{2}$

Beispiel Jurte, 600 cm, 165 cm

Bei einer Jurte mit dem Durchmesser $R=600cm$ und einer Seitenhöhe von $h_{u}=160cm$ ist die benötigte Länge der Stangen bis zum Bund $s=s_{o}+s_{u}={\sqrt {2}}\cdot R+{\sqrt {2}}\cdot h_{u}={\sqrt {2}}\cdot 300cm+{\sqrt {2}}\cdot 160cm=425+226cm=651cm$

Es braucht also Stangenholz mit einer Länge von knapp 7 Metern!

Beispiel Super-Großjurte, 800 cm, 209 cm

Bei einer Super-Großjurte mit dem Durchmesser $R=800cm$ und einer Seitenhöhe von $h_{u}=209cm$ ist die benötigte Länge der Stangen bis zum Bund $s=s_{o}+s_{u}={\sqrt {2}}\cdot R+{\sqrt {2}}\cdot h_{u}={\sqrt {2}}\cdot 400cm+{\sqrt {2}}\cdot 209cm=566+296cm=862cm$

Es braucht also Stangenholz mit einer Länge von knapp 9 Metern!

Ergebnis

Die benötigte Stangenlänge für ein Außendreibein lässt sich recht einfach ausrechnen. Die Formel lässt sich übrigens noch vereinfachen:

Stangenlänge bis zum Bund $s={\sqrt {2}}\cdot (R+h_{u})$ oder über den Daumen geschlagen ohne Taschenrechner $s=1,5\cdot (R+h_{u})$

Wie sicher ist ein Außendreibein?

Außenstangen an einer Jurte sind lang und damit meist auch recht schwer. Beachten solltet ihr, dass ein solches Dreibein sicher steht und nicht plötzlich über schlafenden Kindern zusammen sacken kann.

Die Stangen sollten leicht, aber dennoch stabil sein. Keine zu schwachen oder gar morschen Hölzer verwenden!
Der Dreibeinbund ist fachgerecht und mit geeigneten Seilen auszuführen.
Die Füße des Dreibeins sind gegen wegrutschen zu sichern.
Bei Starkwind oder Sturm ist die Jurte gegebenenfalls zu räumen.
Bei längeren Standzeiten ist die Konstruktion regelmäßig zu überprüfen.

@@ Zeile 1: / Zeile 1: @@
+[[Datei:aussendreibeinfelixbe.jpg|miniatur|Jurte mit Außendreibein, Foto: [https://www.facebook.com/felix.be.1253?fref=ufi&rc=p Felix Be]]]
+[[Datei:aussendreibeinkabe.jpg|miniatur|Jurte mit Außendreibein, Foto: [https://www.facebook.com/kaimahn Ka Be]]]
 [[Datei:aussendreibeinjurte600165.jpg|miniatur|Jurte mit Außendreibein]]
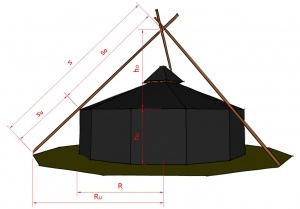
+[[Datei:aussendreibeinformel.jpg|miniatur|Abbildung zur Formel]]
 Um eine [[Jurte]] im Inneren völlig frei von Stangen zu halten, ist ein [[Außendreibein]] eine praktikable Lösung, sofern längeres Stangenholz zu Verfügung steht.
@@ Zeile 5: / Zeile 8: @@
 == Welche Stangenlänge benötigt es hierfür? ==
-Annahme: Aufstellwinkel der Stangen = 45°
+Annahme: Aufstellwinkel der Stangen <math>\varphi = 45^\circ</math>
-In unserer Vorstellung zerlegen wir die benötigte Stangenlänge in einen Teil über der Traufkante einer Jurte und in den Teil unter der Traufkante der Jurte. so betrachten wir einmal einen gedachten Kegel und einmal einen Kegelstumpf.
+In unserer Vorstellung zerlegen wir die benötigte Stangenlänge in einen Teil über der Traufkante einer Jurte und in den Teil unter der Traufkante der Jurte. So betrachten wir einmal einen gedachten Kegel und einmal einen Kegelstumpf.
-In den Formeln heißen diese Strecken für die Stangenlängen Mantellinie.
+In den Formeln für einen Kegel heißen diese Strecken für die Stangenlängen Mantellinie. Diese Formeln findest du in unserer [[Formelsammlung]].
 <math>s_o</math> entspricht der oberen Länge
@@ Zeile 17: / Zeile 20: @@
 <math>R</math> entspricht dem Durchmesser der Jurte
-Für die Höhe des oberen Kegels lautet die Formel <math>h_o = \sqrt{s_o^{2}-R^{2}}</math>. Stellen wir diese Formel um nach <math>s_o</math>, so erhalten wir
+<math>h_u</math> entspricht der Seitenhöhe der Jurte
-== Formeln für einen Kegel ==
+Für die Höhe des oberen Kegels lautet die Formel <math>h_o = \sqrt{s_o^{2}-R^{2}}</math>. Stellen wir diese Formel um nach <math>s_o</math>, so erhalten wir <math>s_o = \sqrt{h_o^{2}+R^{2}}</math>.
-=== gerader Kreiskegel ===
+Nehmen wir nun einen optimalen Winkel mit <math>\varphi = 45^\circ</math> an, so ist <math>h_o = R</math>. Aus unserer Formel wird <math>s_o = \sqrt{{2}}\cdot R</math>
-==== Radius ====
+Nun brauchen wir noch den unteren Teil.
-<math>r = \sqrt{s^{2}-h^{2}}</math>
-==== Höhe ====
+Für <math>s_u</math> gilt <math>s_u = \sqrt{(R_u-R)^2 + h_u^2}</math>. Weiter gilt die Annahme <math>\varphi = 45^\circ</math>. Daraus folgt: <math>R_u = R + h_u</math> und <math>s_u = \sqrt{2}\cdot h_u^2</math>
-<math>h = \sqrt{s^{2}-r^{2}}</math>
-==== Mantellinie ====
+=== Beispiel Jurte, 600 cm, 165 cm ===
-<math>s = \sqrt{h^{2}+r^{2}}</math>
-==== Winkel <math>\varphi</math> ====
+Bei einer Jurte mit dem Durchmesser <math>R = 600 cm</math> und einer Seitenhöhe von <math>h_u = 160 cm</math> ist die benötigte Länge der Stangen bis zum Bund <math>s = s_o + s_u = \sqrt{{2}}\cdot R + \sqrt{2}\cdot h_u =  \sqrt{{2}}\cdot 300 cm + \sqrt{2}\cdot 160 cm = 425 + 226 cm = 651 cm </math>
-eines geraden Kreiskegels ist der halbe Öffnungswinkel, auch ''halber Kegelwinkel'' genannt
-Anwendung der [[Trigonometrische Funktion|trigonometrischen Funktionen]]
+Es braucht also Stangenholz mit einer Länge von knapp 7 Metern!
-<math>\sin\varphi = \frac{\text{Gegenkathete von }\varphi}{\text{Hypotenuse}} = \frac{r}{s}</math>
+=== Beispiel Super-Großjurte, 800 cm, 209 cm ===
-<math>\tan\varphi = \frac{\text{Gegenkathete von }\varphi}{\text{Ankathete von }\varphi} = \frac{r}{h}</math>
+Bei einer [[Super-Großjurte]] mit dem Durchmesser <math>R = 800 cm</math> und einer Seitenhöhe von <math>h_u = 209 cm</math> ist die benötigte Länge der Stangen bis zum Bund <math>s = s_o + s_u = \sqrt{{2}}\cdot R + \sqrt{2}\cdot h_u =  \sqrt{{2}}\cdot 400 cm + \sqrt{2}\cdot 209 cm = 566 + 296 cm = 862 cm </math>
-<math>\varphi = \arcsin\frac{r}{s} = \arctan\frac{r}{h}</math>
+Es braucht also Stangenholz mit einer Länge von knapp 9 Metern!
-==== Durchmesser der Grundfläche ====
+=== Ergebnis ===
-<math>d = 2 \cdot r = 2 \cdot h \cdot \tan\varphi</math>
+Die benötigte Stangenlänge für ein Außendreibein lässt sich recht einfach ausrechnen. Die Formel lässt sich übrigens noch vereinfachen:
-==== Grundfläche ====
+Stangenlänge bis zum Bund <math>s = \sqrt{{2}}\cdot (R + h_u)</math> oder über den Daumen geschlagen ohne Taschenrechner <math>s = 1,5\cdot (R + h_u)</math>
-<math>A_G = r^2\cdot \pi </math>
-==== Flächeninhalt der Mantelfläche ====
+== Wie sicher ist ein Außendreibein? ==
-<math>A_M = r\cdot s\cdot \pi</math>
-==== Oberfläche ====
+Außenstangen an einer Jurte sind lang und damit meist auch recht schwer. Beachten solltet ihr, dass ein solches Dreibein sicher steht und nicht plötzlich über schlafenden Kindern zusammen sacken kann.
-<math>A_O = A_G + A_M = r\cdot\pi\cdot (r + s)</math>
-==== Volumen ====
+* Die Stangen sollten leicht, aber dennoch stabil sein. Keine zu schwachen oder gar morschen Hölzer verwenden!
-<math>V = \frac{1}{3}\cdot \pi\cdot r^{2}\cdot h = \frac{1}{3}\cdot A_G \cdot h</math>
+* Der [[Dreibeinbund]] ist fachgerecht und mit geeigneten Seilen auszuführen.
+* Die Füße des Dreibeins sind gegen wegrutschen zu sichern.
-=== Kegelstumpf ===
+* Bei Starkwind oder Sturm ist die Jurte gegebenenfalls zu räumen.
-[[Datei:01-Kegelstumpf-Definition-Höhe.svg|miniatur|hochkant=0.8|Kegelstumpf,<br />
+* Bei längeren Standzeiten ist die Konstruktion regelmäßig zu überprüfen.
-Definition der Höhe]]
-Mit <math>r</math> werde der [[Radius]] der Deckfläche, mit <math>R</math> der Radius der Grundfläche bezeichnet. <math>\varphi</math> sei der Winkel zwischen einer Mantellinie und der Kegelachse.
-==== Volumen ====
-<math>V = \frac{h \cdot \pi}{3} \cdot (R^2 + R \cdot r + r^2)</math>
-==== Länge einer Mantellinie ====
-<math>m = \sqrt{(R-r)^2 + h^2}</math>
-==== Mantelfläche ====
-<math>M = (R+r) \cdot \pi \cdot m</math>
-==== Deckfläche ====
-<math>D = \pi \cdot r^2</math>
-==== Grundfläche ====
-<math>G = \pi \cdot R^2</math>
-==== Oberfläche ====
-<math>O = \pi \cdot \left[ r^2 + R^2 + m \cdot (r + R) \right]</math>
-==== Höhe des Kegelstumpfs ====
-<math>h=\frac{R-r}{\tan\varphi}</math>

Außendreibein: Unterschied zwischen den Versionen

Aktuelle Version vom 5. Juni 2022, 19:54 Uhr

Inhaltsverzeichnis